Mixing is key to the success of microfluidic devices used in applications from pharmaceutical research to inkjet printers and from drug delivery to food processing. But at the small scales required of microfluidics, where the fluid viscosity is the dominant characteristic, reliable uniform mixing is notoriously difficult to attain.

Molecular diffusion (over time the molecules of two fluids left in contact with one another will diffuse resulting in an homogeneously mixed fluid) may not be practical because of the diffusion coefficient of the fluid in question or the time constraints required of the application. Furthermore, inducing turbulence is not feasible in microfluids.

Currently, microfluid mixing systems are designed largely by trial and error. But fabricating these designs is complicated, expensive and may result consequently in the adoption of less-than-optimal designs.

What is required is a mixing technique for microfluidic systems which is also deterministic causing every part of one fluid to 'visit' every part of the other - known as ergodicity. Dynamical systems theory provides a suitable paradigm for deterministic mixing - chaos. Chaos alone does not guarantee good mixing, but an ergodic, chaotic system does.

At the University of Bristol, Steve Wiggins and Rob Sturman have been researching the mathematics of chaotic microfluidic mixing systems so that optimal designs can be modelled for various applications without resorting to trial-and-error fabrication.

Their research has led them to examine a 25-year old pure-mathematics construct called linked twist maps (LTMs), originally developed by Burton, Easton, Devaney, Przytycki and Wojtkowski in 1980 with no view to practical application.

A twist map describes the motion of points in a system with circulating trajectories where the system is subject to rotation with a shearing effect. Shear means points furthest from the centre of rotation move further in a given time than points closer to the centre. An LTM is obtained when the motion of the system can be described by the repeated alternate application of two (linked) twist maps.

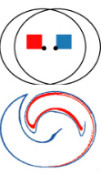
Two blobs, before and after 5 mixing segments, where the flow features underlying the LTM theorems fail to provide good mixing.

Bernoulli mixing

Thorough mixing - whether kneading dough or comparing DNA samples - is essentially a process of stretching and folding the substances so that every part of one visits every part of the other and loses track of its original position. Such a process characterises Bernoulli mixing, the ideal state of a mixed substance.

Bernoulli mixing is usually a hard property to achieve and there are only a few real-world systems that do. LTMs are an example of an artificially constructed system which achieves Bernoulli mixing. Wiggins' and Sturman's work shows how LTMs can be applied to real-world mixing systems.

So how is an LTM applied to a mixing process in the real world?

Let's look at a typical microfluidic mixing problem: DNA hybridisation where two samples of fluid - A and B - containing DNA are mixed to see if they match. If they match, the strands will bond, so the task is to have every strand in sample A visit every strand in sample B.

A recent method is to put the sample A in a chamber with probes for each strand (say up to 10,000), then introduce sample B and use two pumps to transfer the fluids from one side of the chamber to the other, moving them through 90deg after a period of mixing to change the pattern of flow.

However, this typically creates islands of unmixed samples, which, although stretched, don't interact with the surrounding fluid.

The LTM mechanism suggests how to configure the positions of the pumps to achieve optimal mixing.

In the DNA hybridisation example the LTM provides a set of parameters or the theorem to hold and for the fluids to achieve perfect mixing, i.e. for no part of the fluids to be left unmixed.

Wiggins and Sturman have shown that the numerical model holds true and have applied for a UK patent for the system. The next stage is to build a physical model to test the mathematical theory.

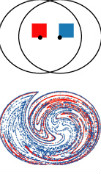
Two blobs, before and after 5 mixing segments, in the case where the flow features underlying the LTM theorems provide good mixing properties.