Multilevel structures and classifications
- Multilevel structures and classifications (PDF, 135kB)
- Multilevel structures and classifications (voiceover with video and slides - Note: to view this presentation you will require to Internet Explorer and Flash player plugin)
This document aims to give a pictionary of basic structures and classifications that underlie multilevel models. We give pictures of common structures, as unit diagrams as classification diagrams, and as words. Note that term classification and level can be used somewhat interchangeably but level implies a nested relationship between sets of units where as classification does not.
You need to decide what are the levels in your data set. Have a look through the sets of examples (1-6) in section A, as you progress through the examples the structures get more complex. Most people will probably have structures similar to one of examples structures given example sets (1 or 2). Then read section B - what is a level? From this you should be able to decide if you have an appropriate data set for multilevel modelling.
Section A: Example Data Structures
Example set 1: Two level nested
For example
- 1.1 pupils within schools
Unit diagram (nodes in diagram are population units)

The same structure as Classification diagram (nodes in diagram are classifications, arrow indicates nested relationship)

Other examples of a two level nested structures:
- 1.2 People within households
- 1.3 Patients within hospitals
- 1.4 Repeated measurements within people (for example growth curves)
Classification diagram Unit Diagram
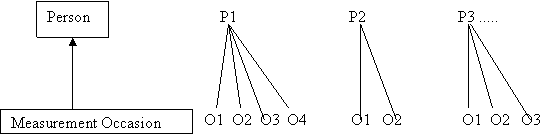
Note that with multilevel repeated measures models individuals can have different numbers of measurement occasions and they can be measured at different times/ages.
- 1.5 Multivariate responses within people. For example, subject (English, French) within pupil. Data need not be balanced, that is not every pupil need have scores for both subjects

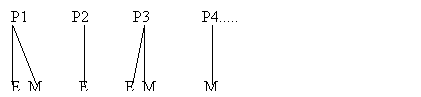
Example Set 2 Three level Nested
For example
- 2.1 pupils within schools within areas
Unit diagram

Classification diagram
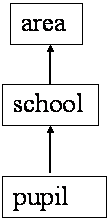
Other examples of a 3 level nested structure
- 2.2 Repeated measures within Pupils within Schools
- 2.3 Multivariate responses within people within households
- 2.4 Pupils within cohorts within schools
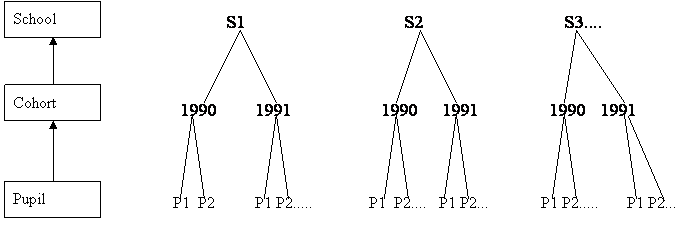
Here the repeated measures are made on the schools. In this case we have scores for groups of pupils who entered school in 1990 and a further group who entered in 1991. The model can be extended to handle an arbitrary number of cohorts. Again the data need not be balanced : every school does not have to have children from both cohorts, within school cohort groups can be different sizes and total number of pupils per school can differ from school to school.
- 2.5 People within cohorts within areas
Example set 3 - Four level Nested
- 3.1 pupil within class within school within LEA
Classification diagram Unit Diagram
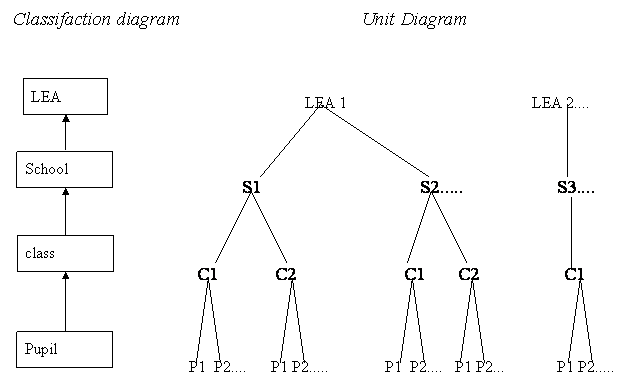
Other examples of four level nested
- 3.2 multivariate responses within repeated measures within pupils within schools
- 3.3 repeated measures within patients within doctor within hospital
- 3.4 people within households within postcode sectors within regions
- 3.5 repeated measures within pupils within cohorts within schools
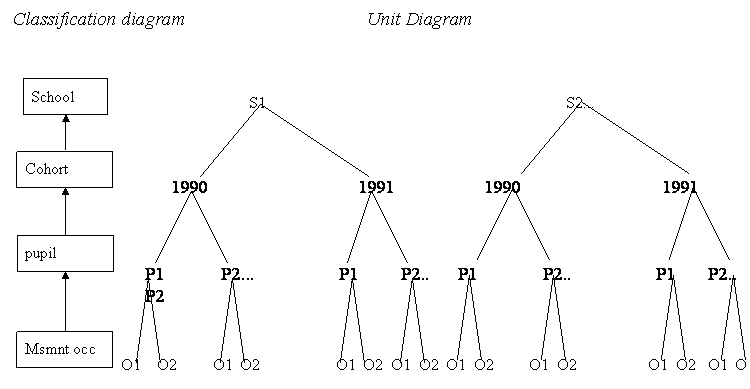
Cohorts are now repeated measures on schools and tell us about stability of school effects over time. Measurement occasions are repeated measures on pupils and can tell us about pupils' learning trajectories. To clarify this consider extending the above diagram to have 4 cohorts pupils starting secondary school in (1990, 1991, 1992, 1993) and children within cohorts are measured every year between the ages of 12 and 16.
| Cohort | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | |
| 1990 | 12 | 13 | 14 | 15 | 16 | |||
| 1991 | 12 | 13 | 14 | 15 | 16 | |||
| 1992 | 12 | 13 | 14 | 15 | 16 | |||
| 1993 | 12 | 13 | 14 | 15 | 16 | |||
Here the black numbers (12..16) are the ages of kids from a cohort at a particular time.
Example set 4 : Non-Nested Models
- 4.1 Two-way cross-classification
Unit diagram where pupils lie within a cross-classification of school by area.
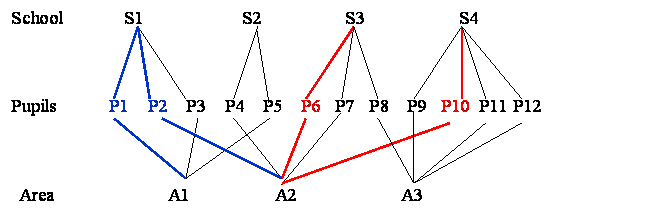
In this structure schools are not nested within areas. For example
- Pupils 1 and 2 attend school 1 but come from different areas
- Pupils 6 and 10 come from the same area but attend different schools
- Area is not nested within school and school is not nested within area
- Pupils lie within a cross classification of school by area.
Classification diagram

Pupil is nested within school and pupils are nested within areas, however school and area are cross-classified so the nodes are not connected.
Other examples of two-way cross-classifications:
- 4.2 Repeated measures within a cross classification of patients by clinician. In a health setting we may a set of repeated measures on patients but patients may be measured by different clinicians at different times. In tabular form
| patient | clinician 1 | clinician 2 | clinician 3 | clinician 4 |
|---|---|---|---|---|
| patient 1 | m1,m2 | m3 | ||
| patient 2 | m2 | m1 | ||
| patient 3 | m3 | m1 | m2 | |
| patient 4 | m1,m2 | m3 |
So patient 1 is seen on measurement occasions 1 and 2(m1 and m2) by clinician 1 and by clinician 4 on measurement occasion 3(m3) and so on.
- 4.3 Exam marks within a cross classification of pupil and examiner. Where a pupil’s paper is marked by more than one examiner to get an indication of examiner reliability.
- 4.4 Pupils within a cross-classification of primary school by secondary school. We may have pupils’ exam scores at age 16 and wish to assess the relative effects of primary and secondary schools on attainment at age 16.
- 4.5 Patients within a cross-classification of GP practice and hospital.
Example set 5 Multiple Membership Models
- 5.1 Pupils multiple members of schools and areas
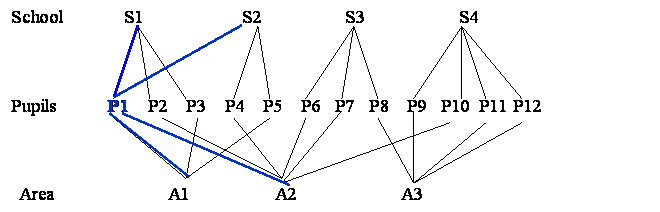
Lets take the structure of pupils within a cross-classification of school by area. But now suppose pupil 1 moves in the course of the study from residential area 1 to 2 a nd from school 1 to 2.
Now in addition to schools being crossed with residential areas pupils are multiple members of both areas and schools.
Classification diagram (double arrow specifies multiple membership relationship)

Other examples of multiple membership relationships
- 5.2 health outcomes where patients are treated by a number of nurses, patients are multiple members of nurses. That is
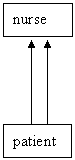
- 5.3 people are multiple members of households
Example set 6
Complex population structures containing mixtures of hierarchies, crossings and multiple membership relationships.
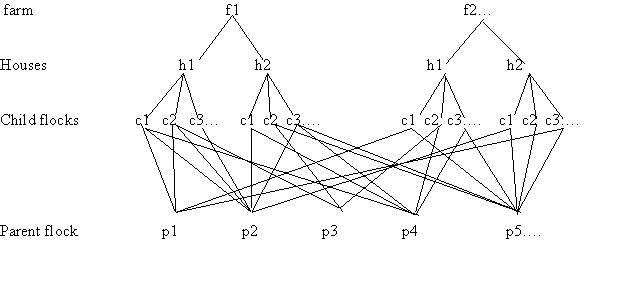
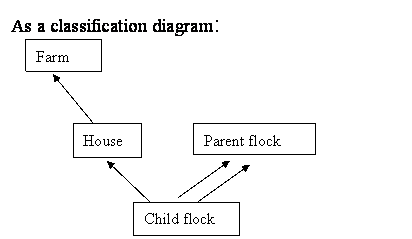
Taking the example from section 11 of the workshop notes
In Denmark Child flocks (10,127) of chickens are reared in houses (725) within farms (304). The child flocks are slaughtered and then another flock of hatched chicks enter the house.
The hatched chicks come from parent flocks (200) who are bred to produce good quality stock. A child flock is made up of chicks from multiple parent flocks.
As a classification diagram:
Section B: What is a level?
The examples in section A have individuals (eg students, doctors, animals), institutions (eg schools, hospitals), area and time (measurement occasion or cohort) as levels. These are some of the more common levels in a multilevel structure.
The key thing that defines a variable as being a level is that its units can be regarded as a random sample from a wider population of units. For example, if we have a multilevel data structure of students within schools, the students are a random sample from a wider population of students likewise the schools are a random sample from a wider population of schools.
Variables, like gender and social class are not levels. This is because they have a small fixed number of categories. For example, gender has only two categories male and female, there is no wider population of gender categories that male and female are a random sample from.
Generally multilevel models are useful for exploring how relationships vary across higher-level units, for example schools.
With nested relationships the higher the level the fewer the number of units at that level.
We number levels from 1, being the lowest, upwards.
- Level 3
- areas, hopitals
- Level 2
- schools, families, doctors, individuals
- Level 1
- students, children, patients, measurement occasions
In practice to do multilevel analysis you need to have at least 20 higher-level units. Note that in example 2.4 in section A of pupils: cohorts: schools, if we have 2 cohort groups per school and 100 schools we do not have 2 units at the cohort group level (level 2) we have 2*100 = 200 cohort groups.
To determine if your data sets is suitable for multilevel analysis firstly identify the levels in the multilevel structure and then check you have at least 20 units at higher levels.
Note: some of the documents on this page are in PDF format. In order to view a PDF you will need Adobe Acrobat Reader
