Reduced order modelling
Staff:
Overview
The unsteady Euler and Navier-Stokes solutions have thousands of degrees of freedom. This means that the costs of unsteady flow studies are prohibitive. Schemes that retain the accuracy of the full non-linear methods, but at a reduced cost will make such studies feasible. This is the rationale for Reduced Order Models (ROMs) that have been, and are being developed at Bristol. Reduced Order Models (ROMs) based on statically non-linear flow solutions, but with a dynamically time linear approach have been developed. Thus unsteady flows that are a small perturbation about a steady flow with shocks and separations are modelled. This makes ROMs ideal for applications such as flutter clearance and aeroservoelasticity. To generate a ROM about a particular non-linear mean solution, the dynamically time linear response must be extracted from the CFD code. At Bristol, this is done by calculating the pulse responses of a linearised version of the code.
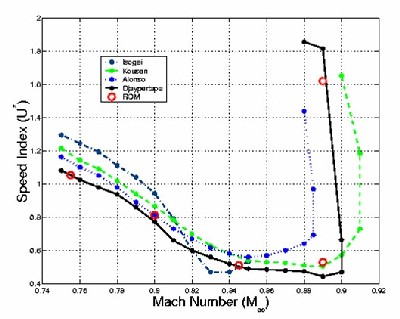
A system identification and reduction scheme is then used to construct the ROM, a state space system, from the pulse responses. This system is of much lower order than the original non-linear CFD scheme, but is able to reproduce its behaviour. The ROMs are in state space form and so can easily be coupled to a structural model for aeroelastic and aeroservoelastic calculations. One advantage of the current approach is that the aerodynamic model is constructed independently of the structural model and thus a redesigned structure does not require a new ROM. The figure below shows that the flutter boundary of a 2D aerofoil can be reproduced by ROMs of order 18, where the original CFD is of order 27,000. The use of ROMs enabled each flutter point to be calculated in less than 1/100th of the computing time compared to the full CFD
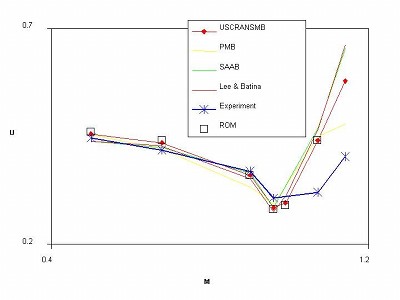
The same ROMs have been used to model the responses to non-linear structural models including models with discrete non-linearities. The identification of the bifurcation diagram (all the possible limit cycle oscillations) is then achievable using continuation. It is only the use of a ROM, with the consequent increase in speed, that makes this computationally feasible. A result for a three-dimensional problem, the AGARD 445.6 test case, is shown below
Current areas of research include: the development of ROM interpolation that will allow the construction of new ROMs from other known ROMs rather than the original CFD. Future areas of research include: development of non-linear ROMs which are able to capture the flow behaviour through local separation and stall.
