Before we plunge headlong into a consideration of the Goldman equation we need to appreciate the limitations of the Nernst potential.
OK, the Nernst equation can calculate the membrane potential (or voltage) which exactly balances a given concentration gradient for an ion. In its classic form it uses a constant of 58 mV which is correct at room temperature (at mammalian body temperature the constant rises to 61 mV). By now you should appreciate that this constant describes the electrical potential difference across a membrane when the membrane separates a 10-fold concentration difference for the permeant ion. So, to remind you again, the Nernst equation has the form (taking K+ as our example):
![]()
However, this is not the whole story. Biological membranes are selectively permeable to more than just potassium. This means that, whilst the diffusion of K+ ions will draw the membrane towards EK (for mammalian cell this will be around -90 mV), the diffusion of other ions, principally Na+, will tend to pull the membrane potential towards ENa which is approximately +60 mV.
Consider this hypothetical case:
A membrane is permeable to K+ and Na+, with EK being -100 mV and ENa being +100 mV. The easiest situation to imagine is one in which the permeability to K+ and Na+ are equal. When you think you know what the membrane potential across this imaginary membrane is click here and see if you are right.
OK, that one is easy to calculate, but if the relative permeabilities are not so convenient it can be difficult to predict the resulting membrane potential. Certainly the Nernst equation cannot help. Well, if we add some terms to the Nernst equation, it can. This new equation is known as the Goldman equation or sometimes the Goldman-Hodgkin-Katz equation. The Goldman equation has the form:
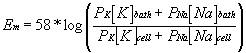
where PK and PNa are the permeability of the membrane to potassium and sodium ions, respectively.
Although under normal physiological conditions the concentration terms of the Goldman equation remain relatively constant, the permeability terms do not. Indeed, large, rapid changes in the ratios of permeability for different ions represent the basis for the action potential and all other electrical events that characterize excitable membranes. On a molecular level, membrane permeability to ions is defined by the activity of membrane channels.